Okasaki's PFDS, Chapter 5
This post contains my solutions to the exercises in chapter 5 of Okasaki’s ‘Purely Functional Data Structures’. The latest source code can be found in my GitHub repo.
Exercise 5.1
- Implement deques.
- Prove that each deque operation takes O(1) amortised time using the potential Φ(f,r)=||f|−|r||.
Solution 5.1
Item 1.
See source.
Item 2.
By symmetry, the costs of cons, head, and tail are (almost) identical to those of snoc, last, and init, respectively.
Consider cons. There is a constant number of actual steps and the potential can change by at most 1. Thus cons runs in constant amortised time.
Consider tail. Any tail which doesn’t empty f requires only one step and changes the potential by one for an amortised cost of ≤2. Any tail which does empty f requires 1+2m+δ steps, where m:=⌊r2⌋, |r|=2m+δ. The linearity is due to the fact that it takes m steps to split r in half, then m more steps to reverse the other half. The change in potential is given by
|1−(2m+δ)|−|m−(2m+δ−m)|=2m+1+δ−δ=2m+1.
Thus, the amortised cost is 1+2m+δ−2m=1, showing that tail runs in constant amortised time.
Exercise 5.2
Prove that insert on binomial heaps runs in O(1) amortised time using the banker’s method.
Solution 5.2
The credit invariant associates one credit to every binomial tree in the heap. Let k be the number of calls to link made by a call to insert. A call to insert takes 1+k actual steps. It initially adds a tree to the heap, gaining a credit, and each link removes a tree, spending a credit. Thus, the total amortised cost is (1+k)+1−k=2.
Exercise 5.3
Prove that the amortised costs of merge and deleteMin are still O(logn).
Solution 5.3
Let hm, hn be binomial heaps with potentials m, n, respectively. We show that the amortised cost of merge is A(hm,hn)≤m+n. Let k be the number of calls to link. The actual cost is bounded by m+n+k, since there can be at most m+n recursive calls to merge and any call reaching the third conditional clause of merge will call link several times via insTree. We start with a potential of m+n, and each call to link reduces this by one, for an end potential of m+n−k. The change in potential is m+n−(m+n−k)=k. Thus, the amortised cost of merge is m+n+k−k=m+n.
Now we show that deleteMin is also logarithmic. We start with a heap hn, which has potential n. There is an actual cost of at most n to find the minimum binary tree, say of rank r. This leaves us with a heap of rank n−1. Then there is an actual cost of at most r to reverse the list of children, making a heap of potential r. Merging these heaps then takes at most n+r−1+k steps, where k is the number of calls to link, which leaves us with a heap with potential n+r−1−k. This is a total of at most n+r+(n+r−1+k) steps. The change in potential is n−(n+r−1−k)=1−r+k. Thus, the amortised cost of deleteMin is
2n+2r+k−1−(1−r+k)=2n+3r−2.
Note that this is indeed logarithmic since, if a heap has a tree of rank r, then it must have at least 2r elements; that is, r=O(logn).
Splay Heaps
A splay heap is a BST that rebalances the tree using a partition function when performing update operations. However, we now allow the insertion of the same element multiple times since we are implementing a heap and not a set.
![h = foldr insert empty [1..7]](../../images/pfds-splayheap-unbalanced.pdf.png)
h = foldr insert empty [1..7]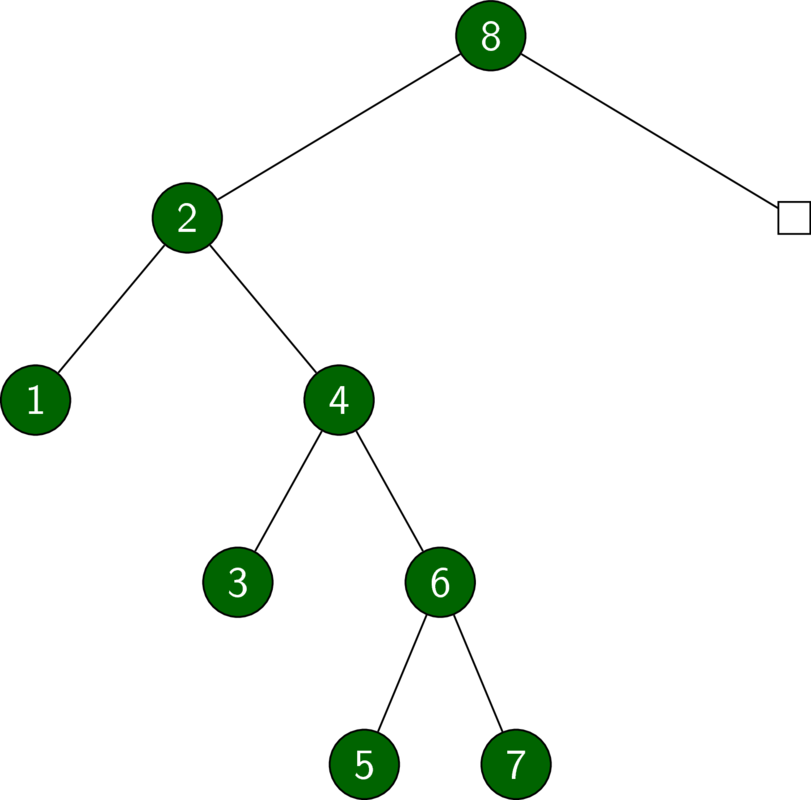
insert 8 hExercise 5.4
Implement smaller.
Solution 5.4
See source.
Exercise 5.5
Prove that partition is logarithmic (in the zig-zag case).
Solution 5.5
First we will need a modification to the lemma proved in the book.
- Lemma
We have the inequality
1+logx+logy≤2log(x+y−1).
for all x∈N≥2, y∈N≥1.
Using the basic logarithmic identities, the above inequality is equivalent to 2xy≤(x+y−1)2. In other words, we must show that x2−2x+(y−1)2≥0 for x≥2, y≥1. The term with y is non-negative. The remaining term x2−2x is non-negative for any x≥2.
□
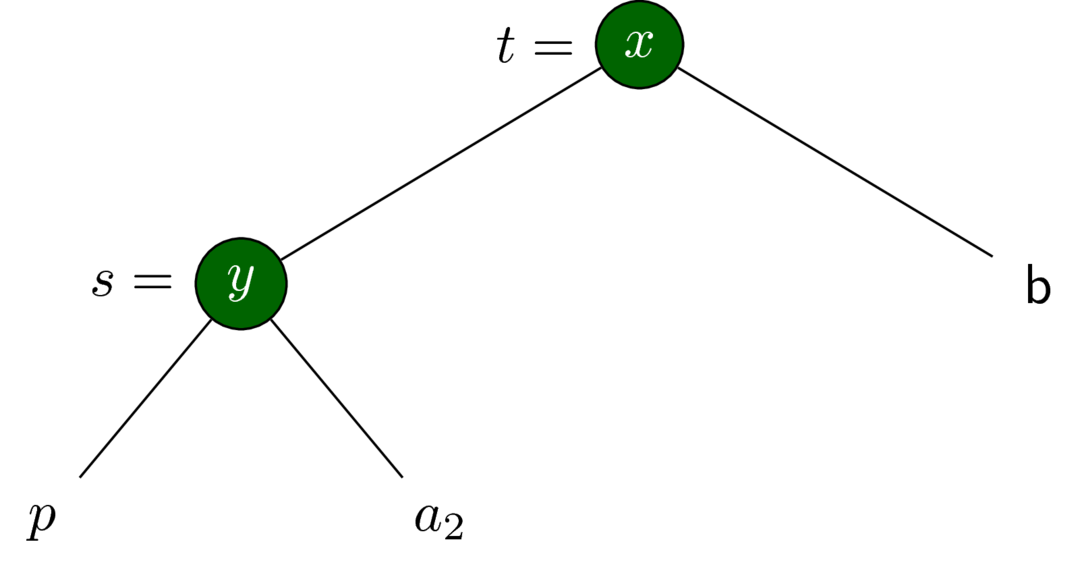
partition pivot t.
partition pivot t outputs (ts,tb).Define (ps,pb) as the output of partition pivot p. Note that #ts+#tb=#t−1, so that 1+ϕ(ts)+ϕ(tb)≤2ϕ(t) by the lemma.
A(t)=T(t)+Φ(ts)+Φ(tb)−Φ(t)=1+T(p)+Φ(ts)+Φ(tb)−Φ(t)=1+A(p)−Φ(ps)−Φ(pb)+Φ(p)+Φ(ts)+Φ(tb)−Φ(t)=1+A(p)−Φ(ps)−Φ(pb)+Φ(p)+ϕ(ts)+Φ(a1)+Φ(ps)+ϕ(tb)+Φ(pb)+Φ(b)−ϕ(t)−ϕ(s)−Φ(b)−Φ(a1)−Φ(p)=1+A(p)+ϕ(ts)+ϕ(tb)−ϕ(t)−ϕ(s)≤2+2ϕ(p)+ϕ(ts)+ϕ(tb)−ϕ(t)−ϕ(s)≤2+ϕ(t)+ϕ(s)+ϕ(ts)−ϕ(tb)−ϕ(t)−ϕ(s)≤2+ϕ(ts)+ϕ(tb)≤1+2ϕ(t)
Exercise 5.6
Prove that deleteMin also runs in logarithmic time.
Solution 5.6
We prove that deleteMin runs in O(3logn) amortised time. Note that #a+(#b+#c)≤#s1 so that 1+ϕ(a)+ϕ(t2)≤2ϕ(s1).
A(s1)=T(s1)+Φ(t1)−Φ(s1)=1+T(a)+Φ(t1)−Φ(s1)=1+A(a)−Φ(a′)+Φ(a)+ϕ(t1)+ϕ(t2)+Φ(a′)+Φ(b)+Φ(c)−ϕ(s1)−ϕ(s2)−Φ(a)−Φ(b)−Φ(c)=1+A(a)+ϕ(t1)+ϕ(t2)−ϕ(s1)−ϕ(s2)≤1+ϕ(a)+ϕ(t1)+ϕ(t2)≤ϕ(t1)+2ϕ(s1)≤3ϕ(s1)
Exercise 5.7
Write a sorting function that inserts elements into a splay tree and then performs an in order traversal of the tree dumping the elements into a list. Show that this function takes linear time in a sorted list.
Solution 5.7
See source.
Let xs be a list of length n in decreasing order. We can measure the complexity of sort xs by counting the number of calls to partition. Every time we call insert x h, we know that x>y for all y in h, so insert x h calls partition exactly once. The function sort xs makes a total of n calls to insert and thus also n calls to partition, showing that sort runs in O(n) time.
The argument for lists in increasing order is completely analogous.
Pairing Heaps
A pairing heap is a heap-ordered multiway tree whose deleteMin operation merges the children in pairs.
![h = foldr insert empty [7, 6..1]](../../images/pfds-pairingheap-wide.pdf.png)
h = foldr insert empty [7, 6..1]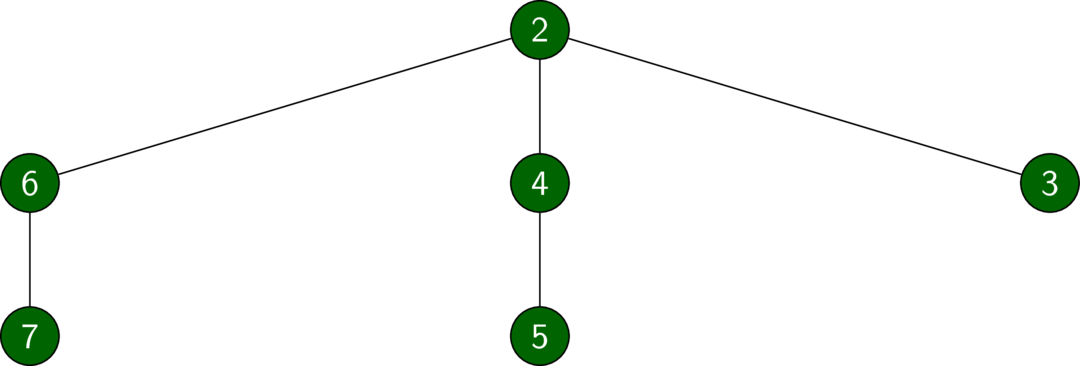
deleteMin hExercise 5.8
Write a function
toBinarythat converts pairing heaps to binary trees.Reimplement pairing heaps using this new representation as binary trees.
Prove that
deleteMinandmergestill run in logarithmic amortised time in this new representation.
Solution 5.8
Item 1.
See source.
The conversion from a pairing heap to a binary tree is explained in the book.
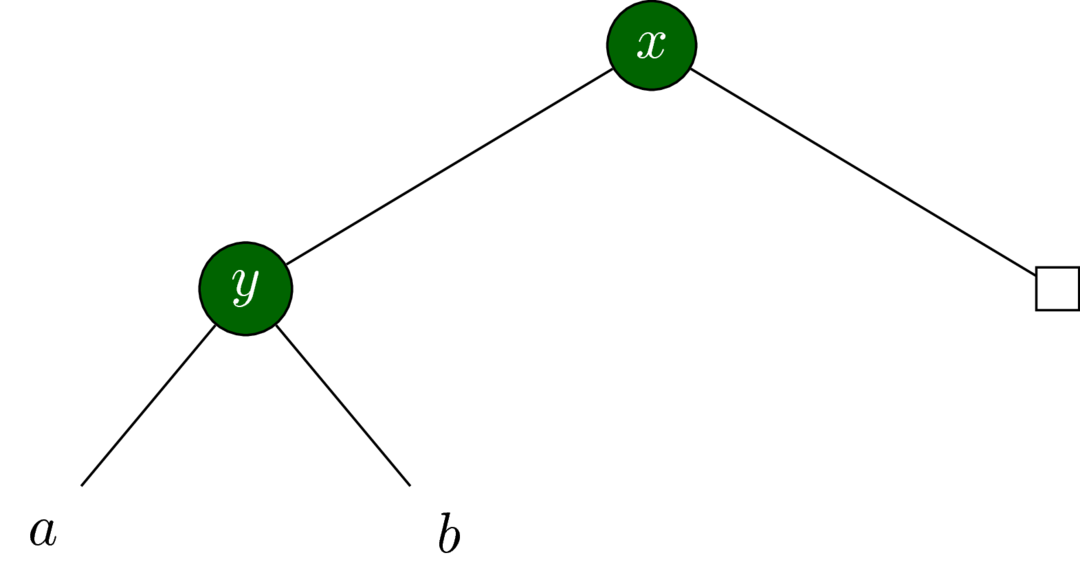
The invariant on a pairing heap T x cs is that x is no greater than any of the elements of its children in cs. This translates into the binary tree invariant that a node is no greater than any of its left descendants. That is, for T' x (T' y a b) c we have that x≤y,ya,yb for all elements ya,yb in the trees a,b, respectively. The value of x bears no relation to the values in c.
We also maintain a second invariant: the right child of the root is empty.
Item 2.
See source.
Remember that the root of a binary tree representation of a pairing heap has no right child (it is empty). Thus we can forget about the right child without losing desired information.
Item 3.
We start with merge. Note that for any x,y≥2, we have log(x+y)≤logx+logy. In particular, #sk≥2.
A(s1,s2)=T(s1,s2)+Φ(t1)−Φ(s1)−Φ(s2)=1+Φ(t1)−Φ(s1)−Φ(s2)=1+ϕ(t1)+ϕ(t2)−ϕ(s1)−ϕ(s2)≤2+2ϕ(t1)≤2+2log(#s1+#s2)≤2+2log(#s1)+2log(#s2)≤2+2ϕ(s1)+2ϕ(s2)
Now consider deleteMin. I was unable to find a nice solution by myself. The following comes from The Pairing Heap: A New Form of Self-Adjusting Heap. We reproduce their argument that the asymptotic cost of deleteMin is A(s1)≤2ϕ(s1)+3.
There are at most 2k+1 calls to merge, where k is the number of children of the root of the pairing heap. The difficult part is calculating the potential increase, which we do in steps.
- Lemma 1
- Let x,y>0 such that x+y≤1. Then logx+logy≤−2.
Proof. This follows from the fact that xy≤x(1−x), which has a maximum of 14 at x=12.
□
- Corollary
We have
log(x+y)−log(y+z)≤2log(x+y+z)−2logz−2,
for any x,y,z≥0.
Proof. By the lemma we have
log(x+y)+logz−2log(x+y+z)=log(x+yx+y+z)+log(zx+y+z)≤−2.
Now
log(x+y)−log(y+z)=log(x+y)+logz−logz−log(y+z)≤2log(x+y+z)−2−logz−log(y+z)≤2log(x+y+z)−2−2logz.
□
- Lemma
- Define s2 to be the tree
T y b cand s1 to be the treeT x a s2.
Then applyingmergeto s1 results in a potential increase of at most 2ϕ(s1)−2ϕ(c)−2.
Proof. Without loss of generality, assume y≤x. Define t2 to be the tree T x a b and t1 to be T y t2 c; that is, t1 is the result of applying merge to s1. The potential increase is Φ(t1)−Φ(s1), by definition. This expands to ϕ(t1)+ϕ(t2)−ϕ(s1)−ϕ(s2), which is equal to ϕ(t2)−ϕ(s2) since ϕ(t1)=ϕ(s1). Now
ϕ(t2)−ϕ(s2)=log(#a+#b)−ϕ(#b+#c)≤2log(#a+#b+#c)−2log(#c)−2=2ϕ(s1)−2ϕ(c)−2.
□
- Corollary
- Define si as the right child of si−1, where s1 is the root of the binary tree, i=1,...,2k−1, and 2k+δ is the length of the right spine of s1. Then the net increase in potential over all calls to
mergein the downwards pass ofmergePairsis bounded by 2ϕ(s1)−2(k−1).
Proof. Applying the previous lemma yields
2ϕ(s2k−1)+k−1∑i=1(2ϕ(s2i−1)−2ϕ(s2i+1)−2)≤2ϕ(s2k−1)−2(k−1)+k−1∑i=1(2ϕ(s2i−1)−2ϕ(s2i+1))≤2ϕ(s1)−2(k−1),
where the last line follows by telescoping the sum.
□
- Lemma
- The net increase in potential over all calls to merge in the upwards pass of
mergePairsis bounded by ϕ(s1).
Proof. Let t be the resulting tree after calling merge on two trees t1,t2. Furthermore, let t′1,t′2 be the subtrees whose roots contain the keys of the trees t1,t2, respectively. Then ϕ(t1)≤ϕ(t′1) and ϕ(t2)≥ϕ(t′2). Thus, the potential increase is bounded by ϕ(t). Since #t=#s1, the potential increase is bounded by ϕ(s1).
□
There are at most 2k+1 actual steps. Removing the root causes a potential increase of −ϕ(s1). The potential increase in the downwards pass in mergePairs is bounded by 2ϕ(s1)−2(k−1). The potential increase in the upwards pass in mergePairs is bounded by ϕ(s1). Therefore, the amortised time is bounded by
2k+1−ϕ(s1)+2ϕ(s1)−2(k−1)+ϕ(s1)=3+2ϕ(s1).
Exercise 5.9
Give examples of sequences of operations for which binomial heaps, splay heaps, and pairing heaps take much longer than indicated by their amortised bounds.
Solution 5.9
For any operation with amortised bounds, we can set up the data structure so that the next execution of that operation is expensive, then call that operation many times.
Binomial Heaps
Binomial heaps support an insert operation with a constant amortised cost. The worst case cost of insert is O(logn), which occurs when inserting into a binomial heap of size 2m−1. In a persistent setting, we can call insert k times on this heap, executing in O(klogn) time instead of O(k).
heap = foldr insert empty [1..(2^m - 1)]
where
m = 7
n = 2^m - 1
tooSlow = map (insert 0) . replicate k $ heap
where
k = 100Splay Heaps
Splay heaps support a findMin operation with a logarithmic amortised cost. The worst case cost of findMin is linear, which occurs after inserting numbers in increasing order into the empty heap. In a persistent setting, we can call findMin k times on this heap, executing in O(kn) time instead of O(klogn).
heap = foldr insert empty [1..n]
where
n = 100
tooSlow = map findMin . replicate k $ heap
where
k = 100Pairing Heaps
Pairing heaps have a deleteMin operation with an amortised cost of O(logn). The worst case cost of deleteMin is O(n), which occurs after inserting numbers in decreasing order into the empty heap. In a persistent setting, we can call deleteMin k times on this heap, executing in O(kn) time instead of O(klogn).
heap = foldr insert empty [n, (n-1)..1]
where
n = 100
tooSlow = map deleteMin . replicate k $ heap
where
k = 100