Okasaki's PFDS, Chapter 2

This post contains my solutions to the exercises in chapter 2 of Okasaki’s ‘Purely Functional Data Structures’. The latest source code can be found in my GitHub repo.

Exercise 2.1

Write a function suffixes of type

suffixes :: [a] -> [[a]]

that takes a list xs and returns a list of all the suffixes of xs in decreasing order of length. For example,

suffixes [1, 2, 3, 4] == [[1, 2, 3, 4], [2, 3, 4], [3, 4], [4], []]

Show that the resulting list of suffixes can be generated in \(\mathcal O (n)\) time and represented in \(\mathcal O (n)\) space.

Solution 2.1

Since there are as many recursive calls to suffixes as there are elements of xs, and both : and tail run in constant time, suffixes must be linear in the length of the list xs. That is, the solution to the recursion \(T (n) = T(n-1) + \mathcal O (1)\) is \(T (n) = \mathcal O (n)\).

Moreover, we use the \(n\) lists that already exist and also \(\mathcal O (n)\) new pointers to each of those lists. Therefore, suffixes xs is represented in \(\mathcal O (n)\) space.

Binary Search Trees (BSTs)

We start with binary trees (not search trees yet!). A binary tree is either empty or has two children, which we call ‘left’ and ‘right’.

data Tree a = E
            | T (Tree a) a (Tree a)
            deriving (Show, Eq)

In the binary trees below, empty nodes are depicted as squares.

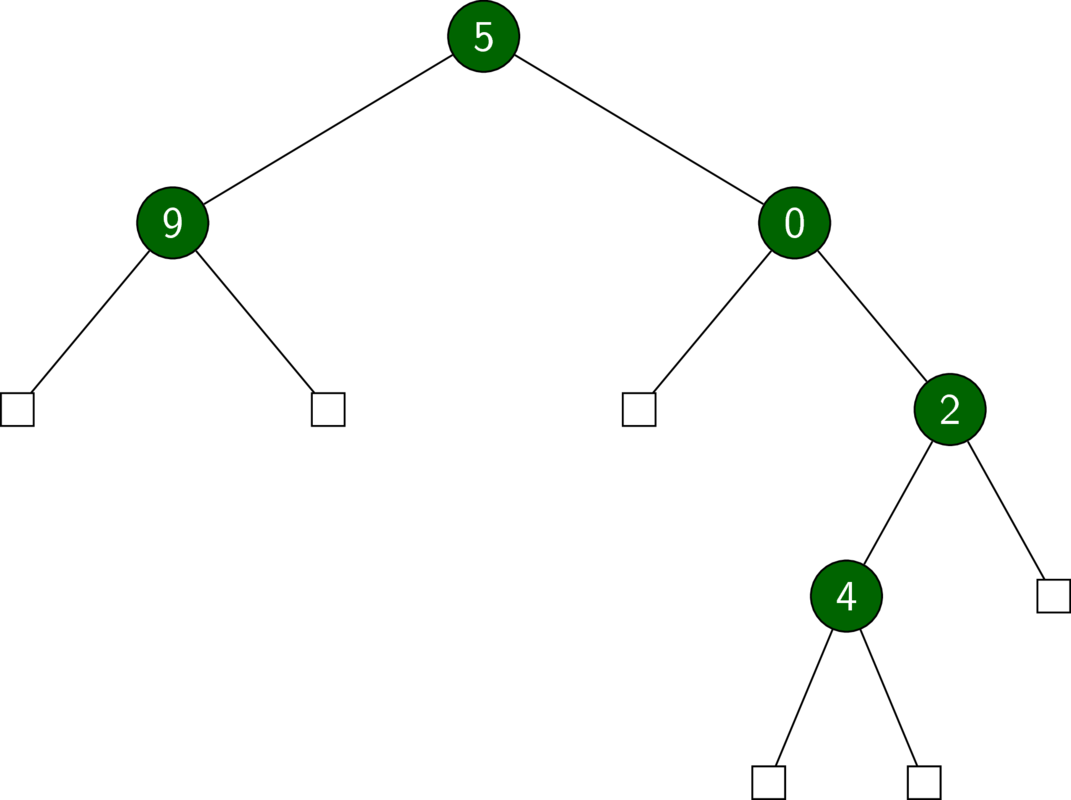
A BST is a binary tree with some extra structure. In particular, we require that the key of a node be greater than that of any of its left descendants and smaller than that of any of its right descendants.

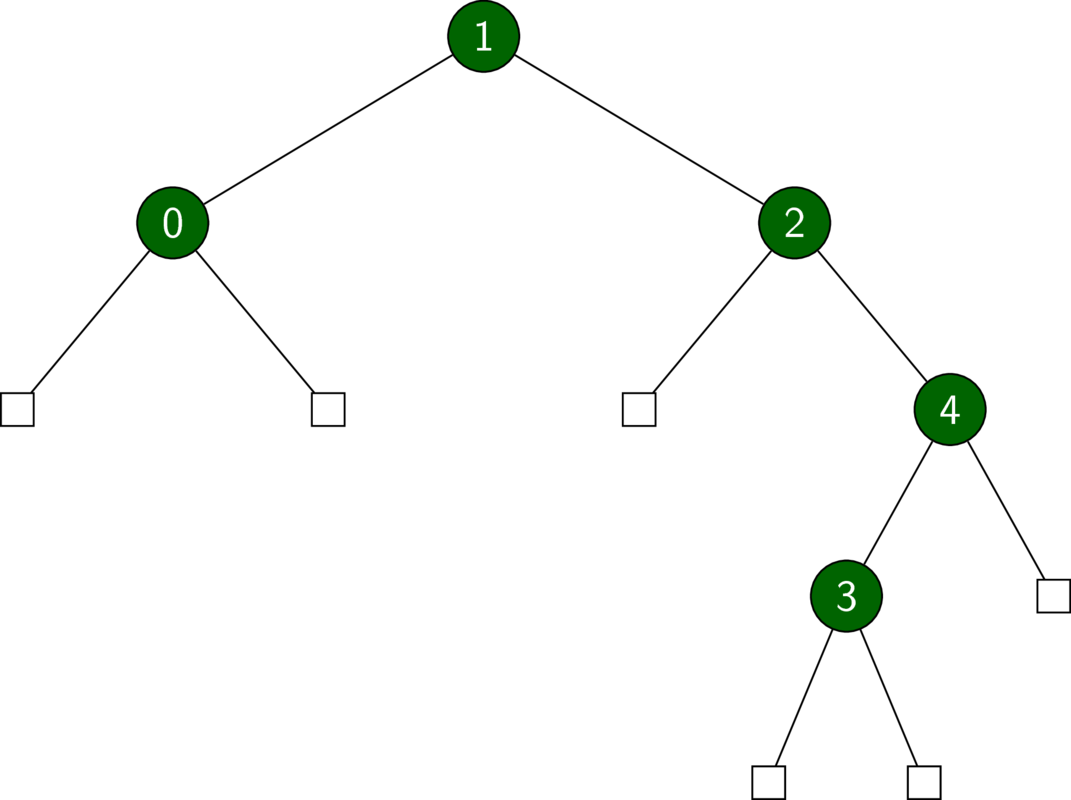
In the following exercises, we implement BSTs in the context of sets.

Exercise 2.2

Rewrite member to take no more than \(d+1\) comparisons.

Solution 2.2

See source.

Exercise 2.3

Rewrite insert using exceptions to avoid copying the entire search path (in the case of inserting an existing element).

Solution 2.3

See source.

We use the Maybe data structure for our errors, i.e. Nothing indicates an error.

Exercise 2.4

Combine the ideas of Exercise 2.2 and Exercise 2.3 to create an insert function that performs no unnecessary copying and uses no more than \(d+1\) comparisons.

Solution 2.4

See source.

Exercise 2.5

1. Write a function complete of type

   complete :: a -> Int -> UnbalancedSet a

   such that complete a d is a complete binary tree of depth d with the key a at every node. This function should run in \(\mathcal O (d)\) time.

2. Extend complete to create balanced trees of arbitrary size that runs in \(\mathcal O (n)\) time, where \(n\) is the number of nodes. A tree is said to be balanced if the size of any node’s left child differs by at most one from the size of that node’s right child.

Solution 2.5

See source.

Item 1.

The recursion is given by \(T(d) = T(d-1) + \mathcal O (1)\), which is solved by \(T (d) = \mathcal O (d)\).

Item 2.

The complexity of balance is equal to that of create2. The recursion for create2 is given by \(T (n) = T (n/2) + \mathcal O (1)\), which is solved by \(T (n) = \mathcal O (\log n)\).

Exercise 2.6

Adapt the UnbalancedSet functor to support finite maps rather than sets. The signature for finite maps is as follows.

class FiniteMap m k a where
  empty  :: m k a 
  bind   :: k ->     a -> m k a -> m k a
  lookup :: k -> m k a -> Maybe a

Solution 2.6

See source.

We reuse the set implementation for UnbalancedSet by creating the Binding data type with the appropriate ordering. Note that this doesn’t allow updating key-value pairs.