BDA3 Chapter 3 Exercise 3

Here’s my solution to exercise 3, chapter 3, of Gelman’s Bayesian Data Analysis (BDA), 3rd edition. There are solutions to some of the exercises on the book’s webpage.

Suppose we have n measurements y∣μ,σ∼Normal(μ,σ), where the prior p(μ,logσ)∝1 is uniform. The calculations on page 66 show that the marginal posterior distribution of μ is μ∣y∼t(ˉy,s/n), where s is the sample standard deviation. The measurements are as follows.

control <- list(
  n = 32,
  mean = 1.013,
  sd = 0.24
)

treatment <- list(
  n = 36,
  mean = 1.173,
  sd = 0.2
)

The t-distribution in base-R is a standardised t-distribution. For a more general t-distribution (with arbitrary location and scale), we’ll use the LaplacesDemon package.

library(LaplacesDemon)

This allows us to plot the marginal posterior means.

mp <- tibble(value = seq(0, 2, 0.01)) %>% 
  mutate(
    ctrl = dst(value, control$mean, control$sd / sqrt(control$n), control$n - 1),
    trt = dst(value, treatment$mean, treatment$sd / sqrt(treatment$n), treatment$n - 1)
  ) %>% 
  gather(cohort, density, ctrl, trt)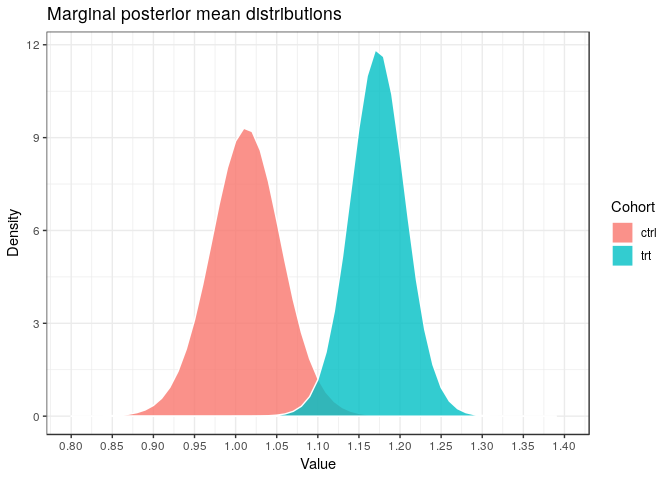 

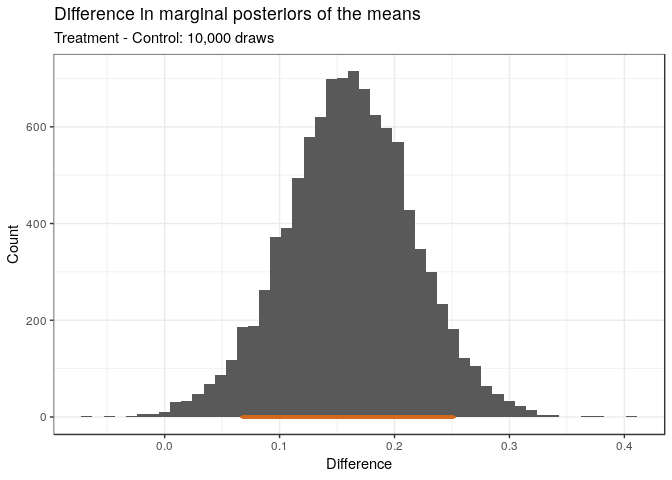
The 95% credible interval of the marginal posterior means is:

draws <- 10000

difference <- tibble(draw = 1:draws) %>% 
  mutate(
    ctrl = rst(n(), control$mean, control$sd / sqrt(control$n), control$n - 1),
    trt = rst(n(), treatment$mean, treatment$sd / sqrt(treatment$n), treatment$n - 1),
    difference = trt - ctrl
  ) 

ci <- difference$difference %>% 
  quantile(probs = c(0.05, 0.95)) 

ci

        5%        95% 
0.06752309 0.25173035 

We can also plot the distribution of the difference.